ANN Search Algorithms
Intro
- 向量检索
- 向量:an n-dim array
- 二值向量:binary vector, n bits
- KNN vs ANN
- Metrics
- Euclidean Distance - Image
- Cosine Similarity - Face Recognition?
- Inner Product - Recommendation
- Hamming Distance - Video
- 基本逻辑:brute-force搜索的方式是在全空间进行搜索,为了加快查找的速度,几乎所有的ANNS方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)子空间,然后在该(几个)子空间里做遍历。

基于树的方法
- KD-Tree
- 从方差最大的维度开始划分(方差大:波动大,划分次数少,深度小)
- 仅适用维度较低的情况(the curse of dimensionality, close to linear when n ~= d)
- Spotify - Annoy
- KD-Tree
- select two centers of mass and get the normal plane, using this plane to segment space. For any new vector x_i, get its inner prodcut with the normal vector of the plane to determine which side of the space it’s in
- 建立多颗子树,提高查询召回率
Hash方法
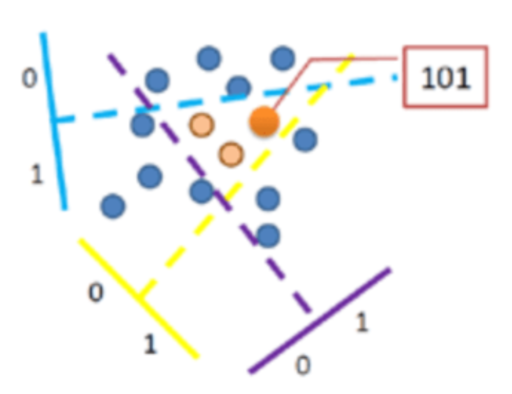
- locality sensitivity: pairs of points that are close together are more likely to collide than pairs of points that are far apart.
- the nearest neigbor will probably lie in the same hash cell (bucket) as the query point. 所以不用brute-force遍历全部的点,只需要比较在同一个cell里的点就有大概率找到query point的NN
- 上图中的划分可以构成一个hashtable,三个partition决定一个cell,同一个cell内的点被存放在hashtable的一个bucket当中
- K=3, since there are 3 partitions (hash functions)
- #cells (bin) of hashtable = 2^K
- 但这样带了一个问题,K的选值问题:
- K太小,cell太少,每个bucket里的点很多,搜索效率很低
- K太大,cell太多,query point和它的NN出现在同一个cell里的概率会变得很低(想象一下把空间切的很碎,那么两个相邻的点就会有非常大的概率至少被一个paritition分开)
- 解决的办法是,采用多个hashtable:
- 对于上图的这种划分,我们的hashtable_2有parition (hash function):p1_1, p1_2, p1_3 (蓝、黄、紫)。那么可以再引入3个partition,p2_1, p2_2, p2_3,重新对空间划分,得到hashtable_2。如此重复L次,得到L个hashtable
- 查询:Given a query, we now perform L independent hash table lookups and get a set of L candidate buckets (one per table). We then use all data points in the L buckets as candidates and compute the distances between the query and each of these points.
- In total, we have K*L partitions (hash functions)
- L的选值问题:
- sweet spot of L: 100~1000
- 这个L太大了,空间消耗太大(hash table太多),查询慢(hash functions计算太多)
- 解决办法:Multiprobe LSH
- The idea is to query more than one bucket in each table. Instead of querying only a single bucket per table (L buckets in total), we now query T > L buckets in total across all tables, where T is a user-specified parameter. A multiprobe scheme chooses these T buckets so that they are (approximately) the most likely buckets to contain the nearest neighbor. So by increasing T, we have a higher probability of finding the nearest neighbor in one of the tables, which allows us to decrease L.
- 例子,向上图中,除了命中到的101以外,还可以选取101临近的bucket,像上方的001
- 得到三个参数
- K,每一个哈希表的哈希函数(空间划分)数目
- L,哈希表(每一个哈希表有K个哈希函数)的数目
- T,近邻哈希桶的数目,即the number of probes
- LSH实现
- LSHash - https://github.com/kayzhu/LSHash
- 基础实现,单个hashtable
- FALCONN
- FALCONN的索引构建过程非常快,百万量级数据,维度如果是128维,其构建索引时间大概2-3min,实时搜索可以做到几毫秒响应时间。
- LSHash - https://github.com/kayzhu/LSHash
https://github.com/FALCONN-LIB/FALCONN/wiki/LSH-Primer
矢量量化方法 PQ
- Vector Quantization - 矢量量化:
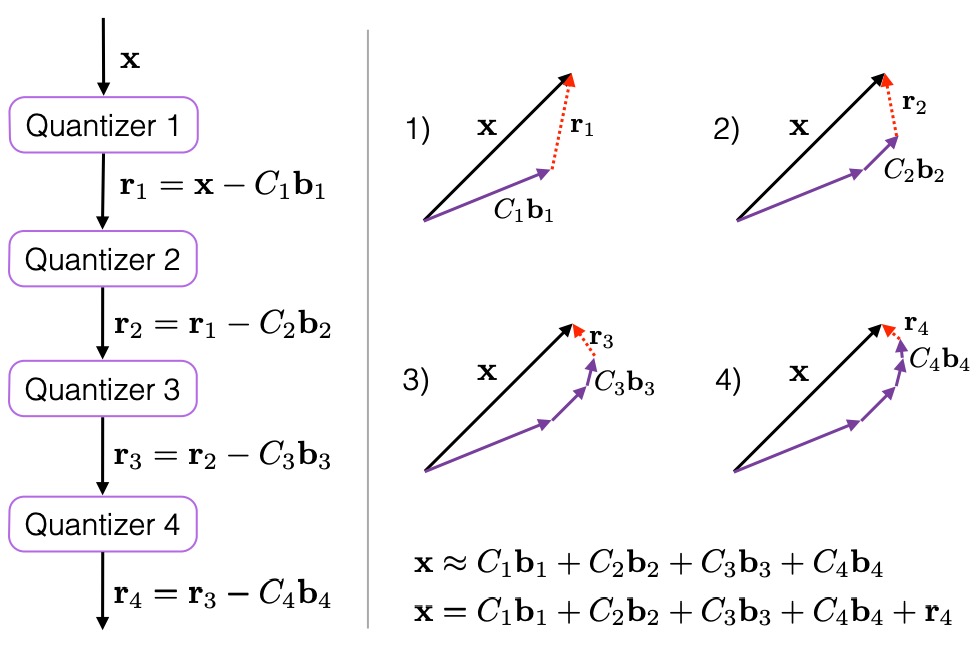
多阶段矢量量化
- Multi-Stage Vector Quantization,MSVQ,或残差矢量量化(Residual Vector Quantization, RVQ)
乘积量化
-
乘积量化(Product Quantization,PQ),乘积量化的核心思想是分段(划分子空间)和聚类
-
建立码本以及量化编码
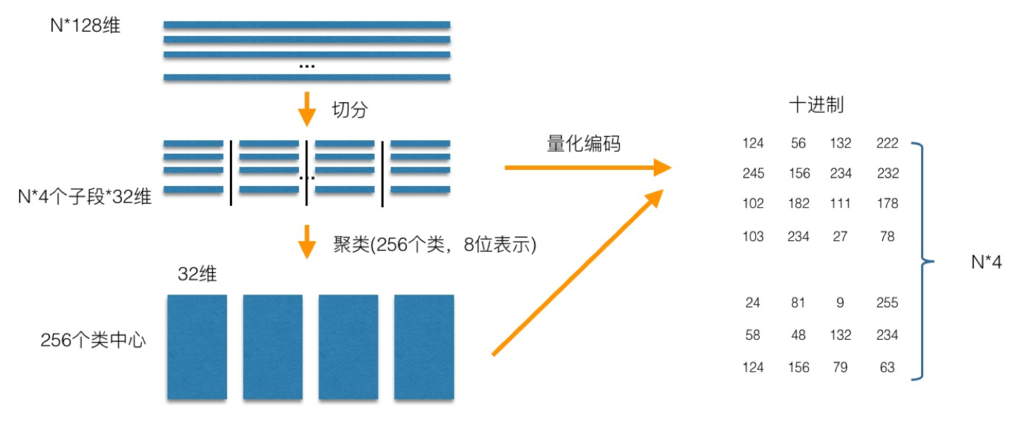
- 训练阶段(索引建立)
- 将128 dims拆分成4子段(32 dims/segment),对每个子段聚类出256个中心点,共有4*256个32 dims的中心点
- 对每个子空间的中心点使用0-255编码,建立码本
- 因此,原来每一个data point,都可以用4个8 bits(256个中心点编号)的编码表示
-
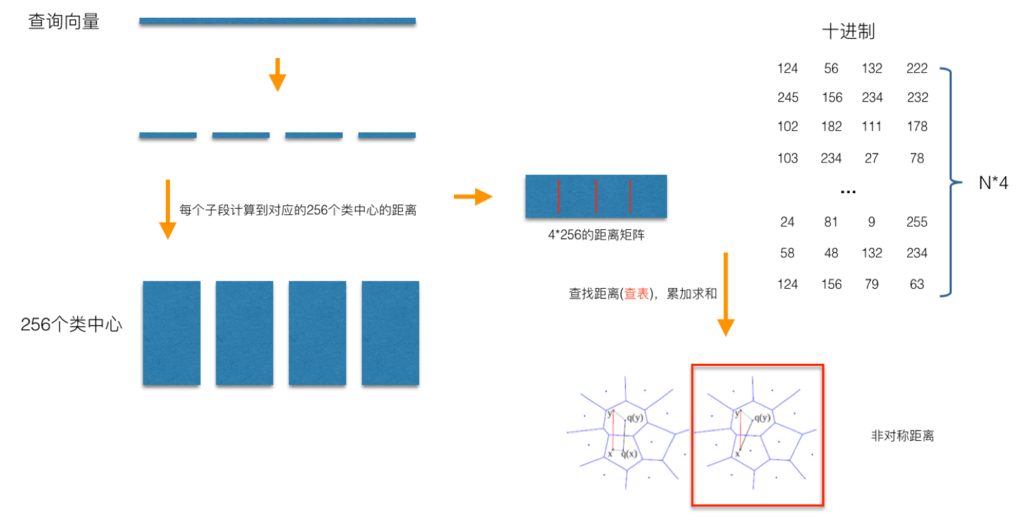
查询样本与dataset中的样本距离计算
-
-
查询
-
-
对称搜索:查询向量q也量化,计算量化后与dataset中其他点的距离
-
非对称搜索:只计算查询向量q与码本中各中心点的距离,得到一个4*256的距离矩阵(距离表)D。与量化后的dataset计算距离时,使用点p的4维编码(p0,p1,p2,p3)和距离表D进行距离计算。则dist(p, q)为
-
dist(p,q) = D[0][p0] + D[1][p1] + D[2][p2] + D[3][p3]
-
-
非对称搜索计算量更小,且更准确(非堆成方法的距离误差上限就是量化器的MSE(q),但对称的距离误差上限为2*MSE(q))
-
-
倒排乘积量化
- 倒排PQ乘积量化(IVFPQ)是PQ乘积量化的更进一步加速版
- IVFPQ原理 - https://zhou-yuxin.github.io/articles/2020/IVFPQ%E7%AE%97%E6%B3%95%E5%8E%9F%E7%90%86/index.html
图索引量化方法 Graph Indexing
- 特点
- 召回率最好,内存消耗相较PQ更大,动态增删不够灵活
- 因为基于图的索引计算近邻关系时,要获取原始特征,需要把特征加载到内存里
- HNSW
- Hierarchical Navigable Small World Graphs
- 基于NSW的改进,通过采用层状结构(类似Skiplist),time complexity从NSW的log^k(n)降到log(n)

-
 - 每层当中,采用贪心遍历,找到query point的NN,再将其作为下一层的entry point,重复NN的搜索
