SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient, Lantao Yu et al.

Paper

Code

直接使用GAN生成序列主要有两个方面的问题：

• GAN适用于生成连续型的而非离散型的数据（如文本序列）。传统的基于Seq2Seq框架的RNN模型，在进行输出的时候，先通过softmax层输出一个vocab_size维度大小的概率分布，再经过argmax sampling得到one-hot vector找到对应词的index。而基于梯度优化后的参数在分布上的微小改变对于直接输入给Discriminator的one-hot vector是无效的。Generator无法做出改进。具体解释参见 [1] 2.2
• GAN难以对不完整的生成序列进行判别。

对于GAN解决离散数据的问题：

• 一种思路是对GAN的计算方式做出调整。Wasserstein-GAN提出用Earth mover’s distance (Wasserstein Metric) 替代JS-Divergence作为真实样本和生成样本分布的度量 [2]。JS-Divergence在两个分布重合部分可忽略不计的情况下（即训练前期）接近常数，无法给出梯度。而Wasserstein Metric的输出要更为平滑 [3]。这样以来，使用WGAN，Discriminator可以直接对比Generator softmax层输出的概率分布和真实样本的one-hot vector，至少在实验中可以生成相对有意义的结果了 [4]。另一种方式将softmax改为gumbel-softmax，其输出可以逼近argmax sampling的输出，从而尽可能的保证分布的重叠 [5]。

• 文章作者采取的办法是将Discriminator作为Reward的来源，对Generator做policy gradient [6]。

  • 

  • Train a \(\theta\)-parameterized generative model \(G_{\theta}\) to produce a sequence,

    \(Y_{1: T}=\left(y_{1}, \ldots, y_{t}, \ldots, y_{T}\right), y_{t} \in \mathcal{Y}\) (the vocabulary of candidate tokens)

    Train a \(\phi\)-parameterized discriminative model \(D_{\phi}\) to provide a guidance

    \(D_{\phi}(Y_{1:T})\) - how likely \(Y_{1:T}\) is from real data or not

  • From the perspective of RL, in timestep \(t\),

    State - \(s = \left(y_{1}, \ldots, y_{t-1}\right)\)

    Action - \(a = y_{t}\)

    Policy - \(G_{\theta}\left(y_{t} \mid Y_{1: t-1}\right)\)

    State Transition is deterministic after an action has been chosen, \(\delta_{s, s^{\prime}}^{a}=1\) for the next state \(s^{\prime} = Y_{1:t}\), if \(s = Y_{1:t-1}\) and \(a = y_{t}\)

  • \(D_{\phi}\) is trained by providing the real sequence data and the synthetic sequences generated from \(G_{\theta}\)

    \(G_{\theta}\) is updated by policy gradient and MC search on the expected end reward from \(D_{\phi}\)

    The reward is estimated by \(D_{\phi}(Y_{1:T})\)

  • 

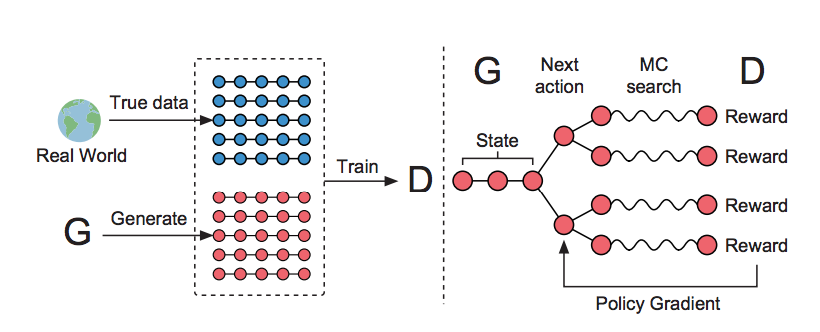
  • Generator’s objective and Policy Gradient

    \[J(\theta)=\mathbb{E}\left[R_{T} | s_{0}, \theta\right]=\sum_{y_{1} \in \mathcal{Y}} G_{\theta}\left(y_{1} | s_{0}\right) \cdot Q_{D_{\phi}}^{G_{\theta}}\left(s_{0}, y_{1}\right)\] \[\nabla_{\theta} J(\theta)=\sum_{t=1}^{T} \mathbb{E}_{Y_{1: t-1} \sim G_{\theta}}\left[\sum_{y_{t} \in \mathcal{Y}} \nabla_{\theta} G_{\theta}\left(y_{t} | Y_{1: t-1}\right) \cdot Q_{D_{\phi}}^{G_{\theta}}\left(Y_{1: t-1}, y_{t}\right)\right]\] \[\theta \leftarrow \theta+\alpha_{h} \nabla_{\theta} J(\theta)\]

  • 采用Monte Carlo Search计算的Reward (action-value function)

    \(Q_{D_{\phi}}^{G_{\theta}}\left(s, a\right)\) is the action-value function of a sequence, i.e. the expected accumulative reward starting from state s, taking action a, and then following policy.

    由于Discriminator只能对完整生成的序列计算reward，因此在序列生成过程中的每一步（\(t \lt T\)），都使用一个roll-out policy \(G_{\beta}\)生成\(N\)个完整的长度为\(T\)的序列，用于估计当前部分生成的序列的reward。

    \[Q_{D_{\phi}}^{G_{\theta}}\left(s=Y_{1: t-1}, a=y_{t}\right)=\] \[\left\{\begin{array}{ll}\frac{1}{N} \sum_{n=1}^{N} D_{\phi}\left(Y_{1: T}^{n}\right), Y_{1: T}^{n} \in \mathrm{MC}^{G_{\beta}}\left(Y_{1: t} ; N\right) \text { for } t \lt T \\ D_{\phi}\left(Y_{1: t}\right) \text { for } t=T\end{array}\right.\]

  • Discriminator’s objective

    \[\min_{\phi}-\mathbb{E}_{Y \sim p_{\text {data }}}\left[\log D_{\phi}(Y)\right]-\mathbb{E}_{Y \sim G_{\theta}}\left[\log \left(1-D_{\phi}(Y)\right)\right]\]

  • The Generative Model for Sequences - RNNs (Seq2Seq)

  • The Discriminative Model for Sequences - Sentence-based CNN

  • 

---

[1] Role of RL in Text Generation by GAN(强化学习在生成对抗网络文本生成中扮演的角色)

[2] Wasserstein GAN

[3] 令人拍案叫绝的Wasserstein GAN

[4] Improved Training of Wasserstein GANs

[5] Categorical Reparameterization with Gumbel-Softmax

[6] SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient