VAE MNIST

---

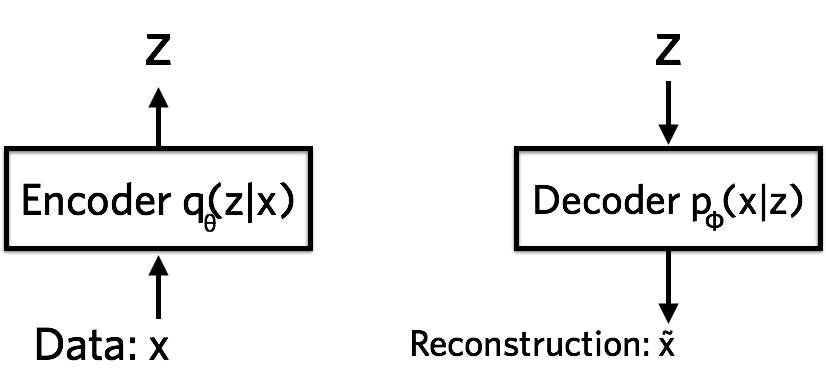
Vanilla VAE

• Loss function (Negative ELBO, NELBO)
  • \[l_i(\theta, \phi) = - \mathbb{E}_{z\sim q_\theta(z\mid x_i)}[\log p_\phi(x_i\mid z)] + \mathbb{KL}(q_\theta(z\mid x_i) \mid\mid p(z))\]
• Reconstructed Loss (Negative Log Likelihood, NLL)
  • \[- \mathbb{E}_{z\sim q_\theta(z\mid x_i)}[\log p_\phi(x_i\mid z)] = l_{i}(\tilde{x_i}, x_i)=-w_{i}\left[x_i \cdot \log \sigma\left(\tilde{x_i}\right)+\left(1-x_i\right) \cdot \log \left(1-\sigma\left(\tilde{x_i}\right)\right)\right]\]
  • \[w_{i} = 1\]
• KL Divergence
  • \[\mathbb{KL}(q_\theta(z\mid x_i) \mid\mid p(z)) = \frac{1}{2}(\log{\sigma_{p}^2} - \log{\sigma_{q}^2} + \frac{\sigma_{q}^2}{\sigma_{p}^2} + \frac{(\mu_{q} - \mu_{p})^2}{\sigma_{p}^2} - 1)\]
  • Assuming the approximate posterior, \(q_\theta(z\mid x_i) = \mathcal{N}{(\mu_{q}, \sigma_{q})}\)
  • Set prior as fixed parameter, \(p(z) = \mathcal{N}{(\mu_{p} = 0, \sigma_{p} = 1)}\)

---

Gaussian Mixture VAE (GM-VAE)

• Loss function (Negative ELBO, NELBO)
  • same as above
• Reconstructed Loss (Negative Log Likelihood, NLL)
  • same as above
• KL Divergence
  • In vanilla VAE, we simply assume that the prior, \(p(z)\), is normally distributed. To get a better performance, in GM-VAE, we instead fit our posterior to \(p(z)\), which is a mixture of gaussian.
  • \[\mathbb{KL}(q_\theta(z\mid x_i) \mid\mid p(z)) = \mathcal{LL}{(z, \mu_{q}, \sigma_{q})} - \sum_{j=1}^{k}{\pi_j \cdot \mathcal{LL}{(z, \mu_{p(j)}, \sigma_{p(j)})}}\]
  • \(\mathcal{LL}\) means log likelihood
  • The second term is log likelihood of gaussian mixture where \(k\) is the number of gaussian components in mixture. In the actual implementation, we simply set the mixture proportion \(\pi = \frac{1}{k}\) for all \(k\) mixture components.
  • For each gaussian component, \(\mathcal{N}{(\mu_{p(j)}, \sigma_{p(j)})}\), \(\mu_{p(j)}\) and \(\sigma_{p(j)}\) are randomly sampled from a standard normal distribution, \(\mathcal{N}(0, 1)\) and are scaled down properly.

---

Experimental Results

Training Curves

VAE

REC loss of VAE

NELBO of VAE

As shown above, simply increasing the size of \(z\) is not always helpful on improving the performance of VAE. Instead, when using a relatively large \(z\) (i.e 1000), it takes much more itertaions (~8k) for the model to reconstruct images well.

GMVAE

REC loss of GMVAE

NELBO of VAE

Test Results

N=20,000	NELBO	REC
VAE, z=10	98.735	79.388
VAE, z=20	96.104	71.958
VAE, z=50	95.947	70.720
VAE, z=100	95.962	70.753
VAE, z=1000	100.170	75.964

N=20,000, z=20	NELBO	REC
GMVAE, k=1	95.159	71.105
GMVAE, k=10	95.029	71.681
GMVAE, k=100	93.431	70.782
GMVAE, k=250	92.741	69.881
GMVAE, k=500	92.397	69.786

Reconstructed and Generated Samples

Reconstructed

VAE, z=20, N=20,000	GMVAE, z=20, k=500, N=20,000

Generated

VAE, z=20, N=20,000	GMVAE, z=20, k=500, N=20,000

GIFs

Random generated samples from VAE (output w/ Bernoulli)

Reconstructed samples from VAE given deterministic MNIST subset (N=20000, z=25)

---

Future Works

• using IWAE bound
• C-VAE
  • Semi-supervised and Full-supervised VAE